Control Structures
Motivating Problem: Temperature Conversions
Scientists and engineers must use several temperature scales in their work. In the United States, most of the public still uses the Fahrenheit scale, while in scientific research the metric scales Celsius and Kelvin are preferred. Modern thermodynamic science postulates a lowest possible temperature for a physical system, which suggests using temperature scales for which 0 corresponds to this lowest possible temperature. The Kelvin scale is the absolute temperature scale in the metric system. Engineers working in the U.S. must often use the Rankine temperature scale, which associates 0 with absolute zero, but where a temperature difference of one Rankine equals one degree Fahrenheit.
Given the need for scientists and engineers to use different temperature scales, creating a computer program that can take a temperature given in one scale by a user and convert it to a temperature in another scale is an important problem. We will need additional ways to control the flow of a program to solve this problem, in particular, we must execute different blocks of code depending on which temperature conversion must be done.
This chapter introduces elements of the programming language that allow for sophisticated program control based on information submitted by the user. We will learn about Boolean expressions and how they are used by the different control structures available in Python.
Definition of Control Structures
Control flow refers to the sequencing of executed statements in a program. A control structure is a type of statement in a programming language that determines the control flow in a program. All programming languages provide the following control structures:
sequential control
selection control
iterative control
Sequential control is the execution of statements one after the other. It is what we have used previously. Selection control involves executing a different block of code depending on the value of a conditional statement, such as one that evaluates to true or false. Iterative control allows for the repetition of a block of statements based on a condition. Figure 1 illustrates these three kinds of control structures.
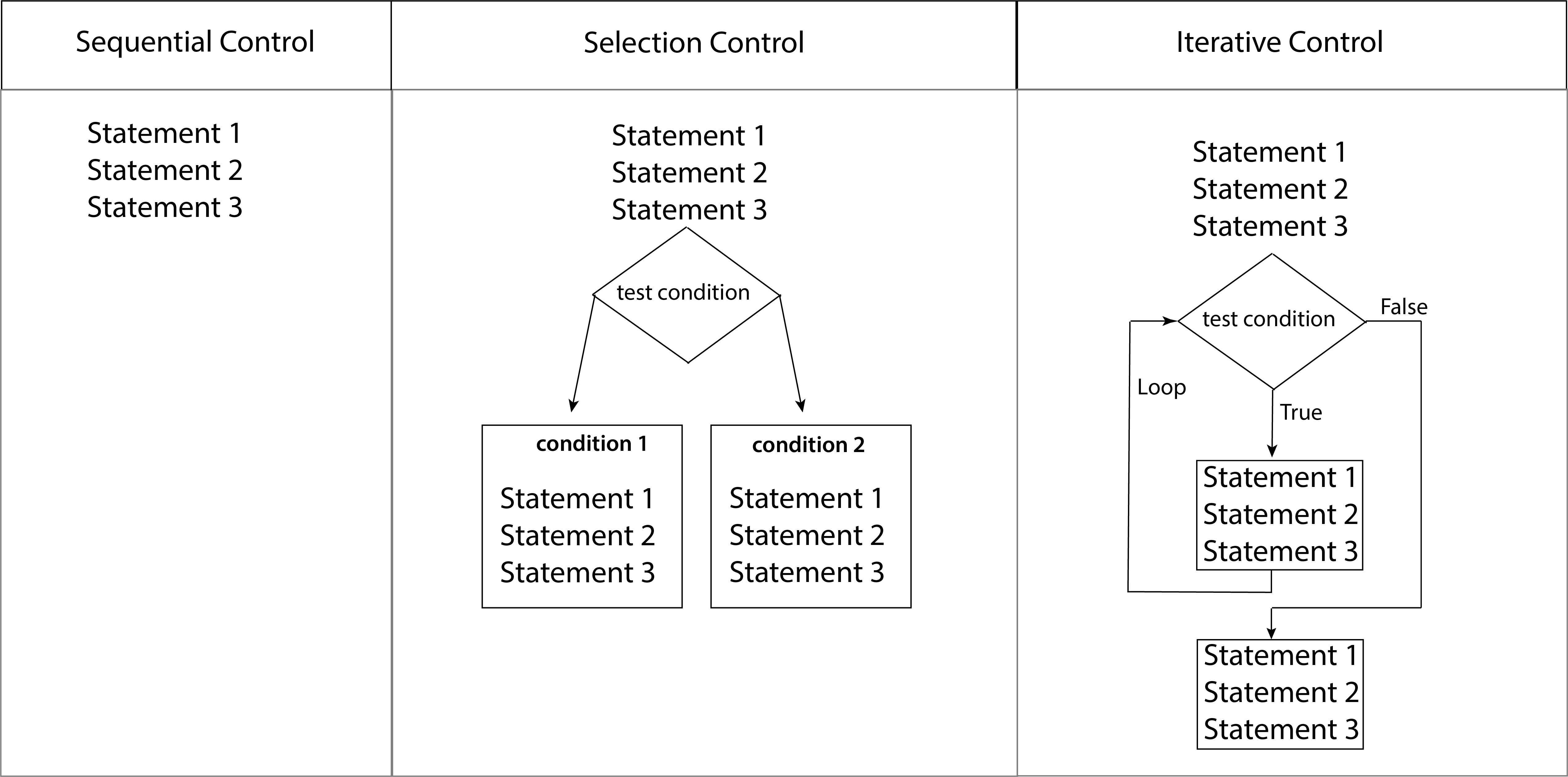
We see in Figure 1 that sequential control involves executing a statement, then executing the next statement, and so on. Selection control shows the program arriving at a decision point where some kind of condition statement is evaluated, often a true/false kind of statement, then the program flow goes to a different code block depending on the value of the condition. Iterative control shows the program arriving at a decision point where a condition statement is evaluated and as long as the condition is true then a code block gets executed in a loop, and when the condition becomes false the program control continues after the loop.
Boolean Expressions
Selection and iterative control often involve a logical expression that evaluates to true or false. Such values are called Boolean data type. Programming languages use Boolean algebra to evaluate expressions involving Boolean variables or values. This type of algebra was developed by the 19th century mathematician George Boole . Instead of operations performed on numbers, as is done in traditional algebra, Boolean algebra involves operations performed on True/False values. We will introduce the Boolean (or logical) operators and, or, and not, and learn how to use them to construct complex Boolean expressions, which always evaluate to either True or False.
In Python, the logical values of true and false are indicated by True and False. The capitalization is important. Also note that the Boolean operators are keywords in Python, so they should not be used as variable names and other identifiers.
The and and or operators are binary operators requiring two Boolean variables or values as operands. The not operator is a unary operator, which simply turns the logical value to its opposite: True becomes False and False becomes True. The result of Boolean operators is defined by the Boolean Truth Table given in Table 1.
| x | y | x and y | x or y | not x |
| FALSE | FALSE | FALSE | FALSE | TRUE |
| TRUE | FALSE | FALSE | TRUE | FALSE |
| FALSE | TRUE | FALSE | TRUE | TRUE |
| TRUE | TRUE | TRUE | TRUE | FALSE |
Relational operators are often involved in Boolean expressions. These operators These operators are used in comparing two values. The Python relational operators are shown in Table 2.
| Operator | Meaning | Example | Result |
| == | equal | 15 == 20 | FALSE |
| != | not equal | 15 != 20 | TRUE |
| < | less then | 15 <20 | TRUE |
| > | greater than | 15 >20 | FALSE |
| <= | less than or equal | 15 <= 15 | TRUE |
| >= | greater than or equal | 15 >= 20 | FALSE |
The relational operators can be applied to any kind of value that has an ordering, including strings. The ordering of string values follows a dictionary ordering based on a particular way of assigning numbers to a character. Python uses the Unicode Standard (Unicode Consortium, 2021) for encoding characters. In this system A is less than B, because the Unicode code for A is 65 and the Unicode code for B is 66. Since the Unicode code for lowercase letters is greater than it is for uppercase letters we have a is greater than B.
We should be careful to avoid errors in using relational operators coming from not distinguishing between meaningful mathematical expressions and meaningful programming language expressions. Consider the following.
\[\label{eq:Equation3.1} 10 < = \text{num} < = 20 \tag{1}\]
Assume that the variable num represents the number 15. The expression is understood in mathematics to mean
\[\label{eq:Equation3.2} \left(10 < = \text{num}\right)\text{and}\left(\text{num} < = 20\right) \tag{2}\]
which evaluates to True, but most programming languages will not make this implicit assumption. Instead the evaluation will proceed as follows.
\[10 < = \text{num} < = 20\rightarrow \left(10 < = \text{num}\right) < = 20\rightarrow \text{True} < = 20\rightarrow \text{error}\]
The final step yields an error since we are trying to compare two different kinds of data, Boolean and numerical. To avoid this problem, you should use parentheses explicitly, as shown in Equation 2.
The Boolean operators must be added to the operator precedence definitions. Table 3 gives the operator precedence order including Boolean operators.
| Operator | Operation | Associativity |
| ** | exponentiation | right-to-left |
| - | negation | left-to-right |
| * , / , // , % | mult , division, trunc, div, modulo | left-to-right |
| + , - | addition , subtraction | left-to-right |
| <,>,<=,>=,!=,== | relational operators | left-to-right |
| not | not | left-to-right |
| and | and | left-to-right |
| or | or | left-to-right |
Parentheses can be used in expressions to help humans reading the code to recognize the desired operator precedence. Consider the expression
\[1 + 2 < 3 + 4\]
The expression is evaluated using the operator precedence order in Table 3 as
\[1 + 2 < 3 + 4\rightarrow 3 < 7\rightarrow \text{True}\]
To assist a human reader of the code the operator precedence could be made explicit by writing the expression as
\[\left(1 + 2\right) < \left(3 + 4\right)\]
Using parentheses in this way is good programming practice.
Selection Control Overview
Selection control allows for different blocks of statements to be executed depending on the value of a conditional expression, often a Boolean expression. We will discuss the Python if statement as the primary example of this control structure. Here is the basic form of the if statement:
if condition:
statement block
else:
statement blockThe condition in this statement must be a Boolean expression, that is one that evaluates to True or False. Also, the else part is optional. Here is a specific example.
if grade >= 70:
print('satisfactory performance')
else:
print('improvement needed') One thing to note about Python syntax is that indentation is important. All statements in a particular statement block must be indented the same amount. To clarify this situation, we must introduce some additional vocabulary. Consider a simplified version of the temperature conversion task. Suppose that the problem is to convert Fahrenheit to Celsius or Celsius to Fahrenheit, depending on what the user specifies. Assume that the user inputs F-C or C-F depending on which conversion must be done. This code will be contained in temp_conversion_type. The temperature to be converted will be in the variable temp_to_convert. The converted temperature will be in the variable converted_temp. Figure 2 introduces some vocabulary to help in discussing control structures.

The header in a control structure is a keyword and ends in a colon. The if statement has two headers. Headers in the same control structure must be indented the same, as seen in Figure 2. A suite or block is a set of statements following a header. They must all be indented the same. The following code will generate an error.
if temp_conversion_type == 'F-C':
converted_temp = (temp_to_convert - 32)*5.0/9.0
print(temp_to_convert,'[F] = ', converted_temp, '[C]')
else:
converted_temp = temp_to_convert*9.0/5.0 + 32.0
print(temp_to_convert,'[C] = ' , converted_temp, '[F]') The amount of indentation of a code block does not matter, although four spaces has become a convention for Python.
Multi-way selection can be achieved by using nested if statements or by using the elif header. Nested if statements have the following structure.
if condition:
statement block
else:
if condition:
statement block
else:
if condition:
statement block
else:
statement blockThe same flow control is achieved more cleanly using the elif header shown in Figure 4.
if condition:
statement block
elif condition:
statement block
elif condition:
statement block
else:
statement blockIterative Control Overview
Iterative control structures allow a block of code to be repeated based on a condition that appears in the header for the structure. As Figure 3.1 suggests, an iterative control structure appears as a loop due to the repetitive nature of the flow. The first iterative control structure that we will introduce is the while loop, which repeatedly executes a code block based on a Boolean expression. The syntax for a while loop is
while condition:
statement blockThe condition must be a Boolean expression that evaluates to True or False. As long as the condition is true, the block of code will execute. When the condition becomes False, the flow control jumps to the first statement after the while loop. Here is a simple example of using the while loop to achieve iterative control:
num = 0
count = 1
number_of_iterations = int(input('Enter the number of iterations:')
while count <= number_of_iterations:
num = num + 1All iterative flow control can be achieved with the while loop, but if the number of iterations is known in advance, then another control structure can be used: the for loop. When this structure is used the loop is executed for each element of a given sequence. We will discuss Python sequence data types in the next chapter, but a commonly used example is provided by the range function.
The range function will produce a sequence of integers that can be used by a for loop. The syntax is
range(start, stop, step)where
start - An integer number specifying at which position to start the integer list. Default is 0. Optional
stop - An integer number specifying at which number to stop. The sequence goes up to but not including this number. Required.
step - An integer number specifying the increment. Default is 1. Optional.
Examples:
range(2,5)generates the sequence
2,3,4
range(5)generates
0,1,2,3,4
range(0,10,2)generates
0,2,4,6,8
The syntax for a for loop is shown below.
for i in sequence:
statement blockThe following example uses the range function to generate a sequence of integers that can be used in a for loop.
for i in range(1,6):
print('Index value is',i)This for loop will produce the following output
Index value is 1
Index value is 2
Index value is 3
Index value is 4
Index value is 5Pseudocode
The Design phase of solving a computational problem can be challenging since it is where we must develop the actual algorithm for the solution. By recognizing the key logical structures of programming without concern with syntax details of a specific programming language we can often work through the basic logic of the solution. One method used by software engineers to construct an expression of this logic is writing pseudocode.
Pseudocode involves using plain language to write out the basic logic of the problem solution using structural conventions of programming languages but not being concerned with specific syntax details. Pseudocode provides a bridge between initial thoughts about a problem solution and an actual working code.
Structural elements of programming languages that we want to recognize in our pseudocode version of the program include control structures and functions. We will use a particular style of writing the pseudocode that recognizes these structural elements.
Let’s start with control structures. There three major kinds of program control: sequential, selection, and iterative. Sequential control involves executing a step and then moving on to the next step, one after the other. In our pseudocode we will always begin a step with a capital letter, as in the following:
Step 1
Step 2
Step 3
.
.
. Selection control involves executing different blocks of code depending on the value of a Boolean conditional variable. This will involve using an if/else type of structure. Our pseudocode style for indicating a selection control block is to make the keywords IF and ELSE uppercase. We will also indicate the end of the IF/ELSE block with the keyword ENDIF.
IF condition
Step 1
Step 2
ELSE
Step 1
Step 2
ENDIF Iterative control involves setting up a loop, which can be done with the while structure or a for loop. Our pseudocode style will require making the appropriate keyword uppercase. The block will end with the keyword ENDWHILE. Here is how the while structure will be indicated:
WHILE condition DO
Step 1
Step 2
ENDWHILEThe for loop will be written as
FOR item IN list DO
Step 1
Step 2
ENDFORWhen we use decomposition and abstraction to help solve a computational problem, we often write separate program units to take care of a particular step in the algorithm. In Python, these program units are typically functions. When writing pseudocode and we decide to make a step of the algorithm into a separate function then we will write a pseudocode version of the function as a separate program unit using the FUNCTION keyword. Important parts of writing the pseudocode for a function are to identify the required parameters passed to the function and the data that will be returned to the main program. We will use the following for the pseudocode style.
FUNCTION function_name
INPUT:parameter1, parameter2
Step 1
Step 2
.
.
.
OUTPUT return_variable1, return_variable2
ENDFUNCTIONWe will indicate the main program in our pseudocode using the PROGRAM keyword.
PROGRAM program_name
Step 1
Step 2
.
.
.
ENDPROGRAMAs an example of developing a pseudocode version of an algorithm, let us consider the problem of cleaning up the yard of a residential property. We start with a high-level view of the algorithm.
PROGRAM clean_up_the_yard
Inspect the yard for debris, excessive grass height, \
unkempt hedges
IF there is debris
Pick up debris
ENDIF
IF there is excessive grass height
Mow the lawn
ENDIF
IF there are unkempt hedges
Trim the hedges
ENDIF
ENDPROGRAMNow we will produce a more detailed version of the algorithm, as shown in Figure 12. Note that for each of the steps listed in the pseudocode of Figure 11 we add additional detailed steps.
PROGRAM clean_up_the_yard
Inspect the yard for debris, excessive grass height, \
unkempt hedges
IF there is debris
Determine the kind of debris
IF debris is mainly leaves
Get some 30 gallon yard bags
Rake up leaves
Put leaves in bags
ELSE
Get the wheelbarrow
WHILE debris remains DO
Fill up wheelbarrow
Empty wheelbarrow at wood pile
ENDWHILE
ENDIF
ENDIF
IF there is excessive grass height
Get the lawn mower
Check the gas
IF mower needs gas
Fill the gas tank
ENDIF
WHILE the lawn is not finished DO
Mow a lap
ENDWHILE
ENDIF
IF there are unkempt hedges
Get the hedge clippers
Trim the hedges
ENDIF
ENDPROGRAMComputational Problem Solution: Temperature Conversion
We return to the temperature conversion problem described at the beginning of this chapter. We will develop a program that solves this problem using programming elements developed in the chapter.
Analysis
The first step in problem analysis is to state the problem precisely and describe how to recognize a successful solution.
Problem Statement: The program requests that the user submit a temperature including scale used and also requests to which scale the temperature should be converted. The Program should perform some error detection to ensure that the submitted temperature is not below absolute zero on the user chosen scale. The program will print out the converted temperature with appropriate label. Temperature scales that will be used are Celsius, Fahrenheit, and Kelvin. Temperatures should be formatted to show two digits right of the decimal point.
Part of our analysis is to research physical principles that may be helpful in solving the problem. In this case, we can look up absolute zero for each of the scales being considered. These temperatures are shown in Table 4.
| Scale | Absolute Zero |
|---|---|
| Celsius | -273.15 |
| Fahrenheit | -459.67 |
| Kelvin | 0 |
We continue our background research to find the equation for each of the required conversions. Equation 3 through Equation 8 show the required conversion equations.
\[ T_C = T_K- 273.15 \tag{3}\]
\[ T_C = \left(T_F- 32\right) \times \frac{5}{9} \tag{4}\]
\[ T_F = \frac{9}{5} \times T_C + 32 \tag{5}\]
\[ T_F = \left(T_K- 273.15\right) \times \frac{9}{5} + 32 \tag{6}\]
\[ T_K = T_C + 273.15 \tag{7}\]
\[ T_K = \left(T_F- 32\right) \times \frac{5}{9} + 273.15 \tag{8}\]
These equations can be used to generate some test data that will be used to with our program. This allows us to recognize a program that works correctly. Table 5 shows relevant test data.
| Submitted Temperature | Converted Temperature | ||
| T | Scale | T | Scale |
| -300 | C | Error | |
| -150 | C | -238 | F |
| -150 | C | 123.15 | K |
| 0 | C | 32 | F |
| 0 | C | 273.15 | K |
| -500 | F | Error | |
| -400 | F | -240 | C |
| -400 | F | 33.15 | K |
| 0 | F | -17.78 | C |
| 0 | F | 255.37 | K |
| -100 | K | Error | |
| 0 | K | -273.15 | C |
| 0 | K | -459.67 | F |
| 150 | K | -123.15 | C |
| 150 | K | -189.67 | F |
Design
The solution design for our problem should include a description of the algorithm using pseudocode and a list of the required data structures (variable names and types) used in the code. Table 6 shows the required variables for implementing the algorithm for this problem solution. Typically, we would start this table as we begin to think about the algorithm and then add to it as the algorithm develops.
| Data Structure | Type | Description |
|---|---|---|
| submission_is_incorrect | Boolean variable | specifies whether submitted temperature is above absolute zero |
| submitted_temperature | float variable | temperature submitted by user |
| submitted_scale | string variable | scale for submitted_temperature |
| converted_temperature | float variable | the converted temperature |
| converted_scale | string variable | scale for converted_temperature |
Python uses a preferred style for creating variable names (Rossum et al., 2022). This style recommends that variable names (and function names) be all lower case with individual words in the name separated by an underscore. We should note that other programming languages use different style conventions and companies that use Python for software development will sometimes have a different style guide. We will use the PEP 8 recommended style in this book.
After starting the list of required data structures (variable names, in this case), we write out a high-level pseudocode version of the algorithm, as shown in Figure 13.
PROGRAM temperature_conversion
Print a program greeting
submission_is_incorrect = True
WHILE submission_is_incorrect DO
Request that the user submit a temperature to convert
(defines submitted_temperature)
Request that the user submit the scale of submitted
temperature (defines submitted_scale)
Check whether submitted_temperature is above absolute zero
IF submitted_temperature is above absolute zero
submission_is_incorrect = False
ENDIF
ENDWHILE
submission_is_incorrect = True
WHILE submission_is_incorrect DO
Request that the user submit a scale for the conversion
(defines convertedScale)
IF convertedScale is okay
submission_is_incorrect = False
ENDIF
ENDWHILE
Calculate converted_temperature
Print out converted_temperature
ENDPROGRAMNote that the while loops implement our error detection for submitted input.
Implementation
We will now create a Python code implementation of each part. The program greeting and first while loop that checks for a correct temperature submission is shown in Figure 14 Note that the program code starts with a brief documentation comment, which includes a few key items such as the author, a version number, and a brief summary of what the program does. This is a good step towards providing documentation for the program. In addition to the iterative control structure (while loop), this section uses the mult-way selection structure (if elif).
"""
Program Name: Temperature Scale Conversion
Author: C.D. Wentworth
version: 6.23.2022.1
Summary: Temperature Conversion Program with Input error checking of
temperatures. This version accepts a user-defined temperature in
Celsius, Fahrenheit, or Kelvin and converts the temperature
to a user selected scale.
"""
# Display program greeting
print('Welcome to the Temperature Scale Conversion Program!')
print('This program will request that the user submit a temperture.')
print('Next, it requests the converted scale.')
print('Finally, it prints out the converted temperature.')
submission_is_incorrect = True
scale_request = "'C' for Celsius, 'F' for Fahrenheit, 'K' for Kelvin"
while submission_is_incorrect:
submitted_temperature = float(input('Submit a temperature to convert: '))
print('Specify the scale of your submitted temperature: ')
submitted_scale = input(scale_request)
if ((submitted_scale =='C') and (submitted_temperature>=-273.15)):
submission_is_incorrect = False
elif ((submitted_scale == 'F') and (submitted_temperature>=-459.67)):
submission_is_incorrect = False
elif ((submitted_scale == 'K') and (submitted_temperature>=0)):
submission_is_incorrect = False
else:
print('Incorrect submitted temperature. Try again.')
Next, we code the program part that requests that the user submit a temperature scale for the converted temperature. The while loop provides for some user input error detection.
print('What scale should be used for the converted temperature?')
converted_scale = input(scale_request)
submission_is_incorrect = True
while submission_is_incorrect:
if ((submitted_scale == 'C') and
(converted_scale == 'F' or converted_scale == 'K')):
submission_is_incorrect = False
elif ((submitted_scale == 'F') and
(converted_scale == 'C' or converted_scale == 'K')):
submission_is_incorrect = False
elif ((submitted_scale == 'K') and
(converted_scale == 'C' or converted_scale == 'F')):
submission_is_incorrect = False
else:
print('There is a problem with your submission.')
converted_scale = input(scale_request) Finally, we code the actual temperature conversion calculation and print out the result.
if submitted_scale == 'C':
if converted_scale == 'F':
# convert Celsius to Fahrenheit
converted_temperature = submitted_temperature*9.0/5.0 + 32.0
else:
# convert Celsius to Kelvin
converted_temperature = submitted_temperature + 273.15
elif submitted_scale == 'F':
if converted_scale == 'C':
# convert Fahrenheit to Celsius
converted_temperature = (submitted_temperature - 32.0)*5./9.
else:
# convert Fahrenheit to Kelvin
converted_temperature = (submitted_temperature - 32.0)*5.0/9.0 + 273.15
else:
if converted_scale == 'C':
# convert Kelvin to Celsius
converted_temperature = submitted_temperature - 273.15
else:
# convert Kelvin to Fahrenheit
converted_temperature = (submitted_temperature - 273.15)*9.0/5.0 + 32.0
# print out the result
s1 = format(submitted_temperature,'.2f')
s2 = format(converted_temperature,'.2f')
print(s1,submitted_scale,' is ', s2,converted_scale)Testing
Table 5 gives some test data to use with the program. We reproduce that table below Table 7 and add a column giving the actual program output. Since the output column matches the expected converted temperature column we have some evidence that the program runs correctly.
| Submitted Temperature | Converted Temperature | |||
|---|---|---|---|---|
| T | Scale | T | Scale | Program Output |
| -300 | C | Error | error detected | |
| -150 | C | -238 | F | -238 |
| -150 | C | 123.15 | K | 123.15 |
| 0 | C | 32 | F | 32 |
| 0 | C | 273.15 | K | 273.15 |
| -500 | F | Error | error detected | |
| -400 | F | -240 | C | -240 |
| -400 | F | 33.15 | K | 33.15 |
| 0 | F | -17.78 | C | -17.78 |
| 0 | F | 255.37 | K | 255.37 |
| -100 | K | Error | error detected | |
| 0 | K | -273.15 | C | -273.15 |
| 0 | K | -459.67 | F | -459.67 |
| 150 | K | -123.15 | C | -123.15 |
| 150 | K | -189.67 | F | -189.67 |
Exercises
1. Describe the three kinds of program flow control.
2. What is the value of each of the following Boolean expressions?
- 10 >= 20
- 10 != 20
- (10 >= 20) and (10 != 20)
- (10 >= 20) or (10 != 20)
- ‘Jim’<‘Mike’
- 12*2 == 8*3
3. Correct the indentation in the following code block so that it will execute without an error.
score = 81
if score >= 90:
print('Your score indicates outstanding work.')
elif score >=80:
print('Your score indicates good work.')
print('You can resubmit your work.')
elif score >=70:
print('Your work is adequate.')
print('Try to improve your score.')
else:
print('Your work needs improvement.')
print('Please try again.')4. Develop an algorithm, and pseudocode implementation of it, for the problem of cleaning an apartment with multiple bedrooms. Produce two versions: a high-level version with not many details, and then a more detailed version.
Program Modification Problems
1. In this exercise you are given a program (shown below) that obtains two integers from the user and then prints a message depending on whether the integers are both zero or not. You must change the code so that it tests whether both integers are zero, one is zero and one is non-zero, or both are non-zero and prints an appropriate message.
[ language=Python , numbers=none , backgroundcolor=\color{light-gray}] """
Program Name: Chapter 3 Prog Mod Prob 1
Author: C.D. Wentworth
version: 6.23.2022.1
Summary: This program requests that the user
submit two integers and then
determines whether one is zero or
not and then prints a message.
"""
# Ask user for two integers
i1 = input('type in an integer ')
i1 = int(i1)
i2 = input('type in another integer ')
i2 = int(i2)
if i1 == 0 or i2 == 0:
print('One of the integers is zero')
else:
print('Neither integer is zero')2. Add the Rankine temperature scale to the available scales in the Temperature Scale Conversion Program. Remember to check that the temperature submitted by the user is greater than or equal to absolute zero.
References
Rossum, G. van, Warsaw, B., & Coghlan, N. (2022). PEP 8 – Style Guide for Python Code peps.python.org. https://peps.python.org/pep-0008/
Unicode Consortium. (2021). Unicode. Unicode. https://home.unicode.org/