Functions
Computer applications used in science and engineering can involve thousands or millions of lines of code. Faced with the complexity of such programs, programmers can use the computational science pillars of abstraction and decomposition to create a high-level conceptualization of the program and then break the coding into more manageable pieces. One method of applying the ideas of abstraction and decomposition is to use named blocks of code or program routines. In Python, program routines are called functions.
Functions will aid in managing code complexity and achieving code modularity: creating code that can be used to solve multiple computational problems. In this chapter, we will learn how to create user-defined functions and become familiar with underlying computer science concepts that will help us use functions correctly in a program.
Motivating Problem: Temperature Conversion –Revised
In Chapter 3, we developed a program to perform user-requested temperature conversions, such as going from Fahrenheit to Celsius. While the code structure is evident due to added comments, we can improve the clarity by defining functions to perform parts of the program, such as requesting a temperature from the user and performing the temperature conversion. Having functions for these tasks will allow us to reuse some of the code in other programs. Therefore, the problem we want to solve is to rewrite the code from Chapter 3 so that the following tasks are performed in their own separate functions:
request a temperature to convert from the user
request the final temperature scale to be used
perform the actual temperature conversion calculation
Program Routines
A computer program can contain a block of code that gets repeated. We have seen that iterative control structures do this. If the block contains many lines of code, then the program’s design can be clarified by bundling the block into a separate part that a single line of code can substitute. A block of code that a name can reference is called a program routine. A routine can be called up and executed as often as required by just using the name. Figure 1 shows the concept of reusing a named block of code. Figure 2 shows how a code block in a program can be replaced by a single code line using a program routine. Program routines are called functions in Python.
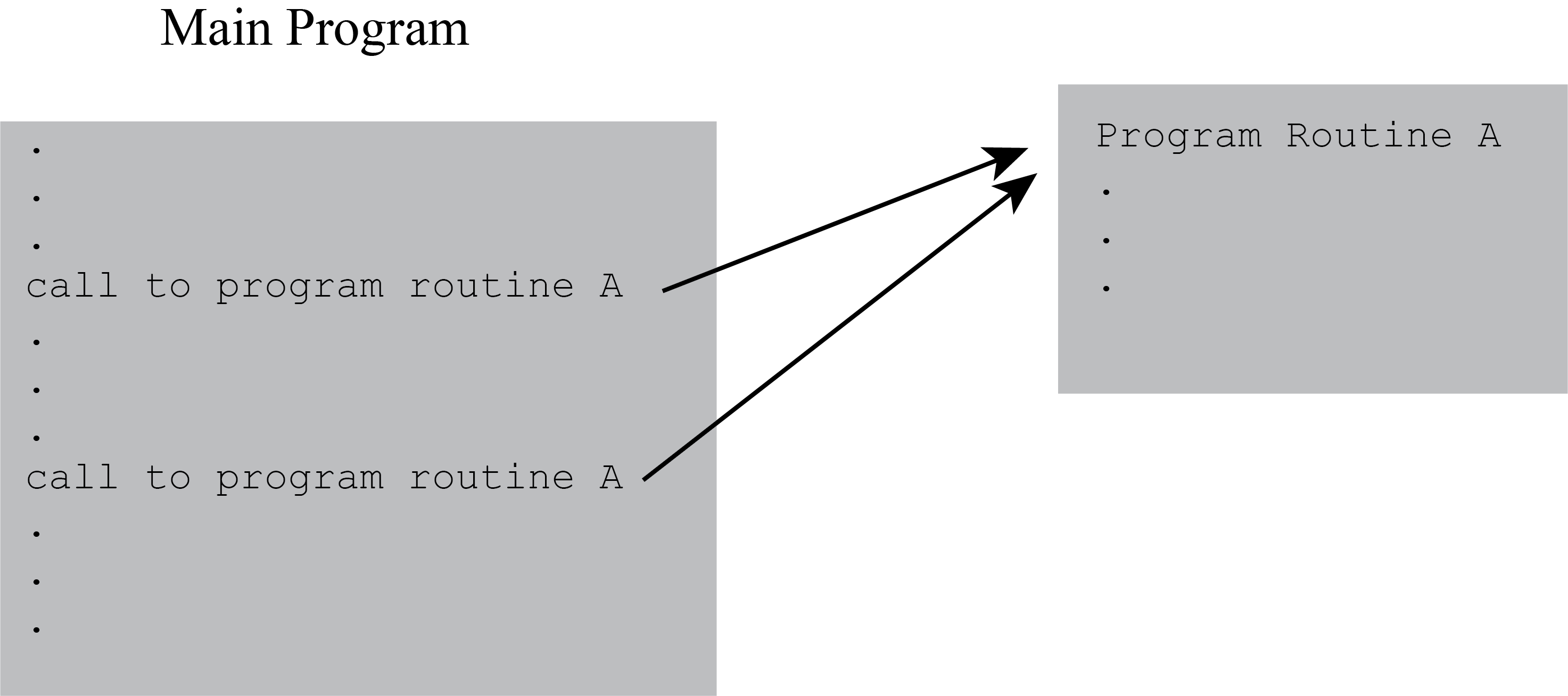
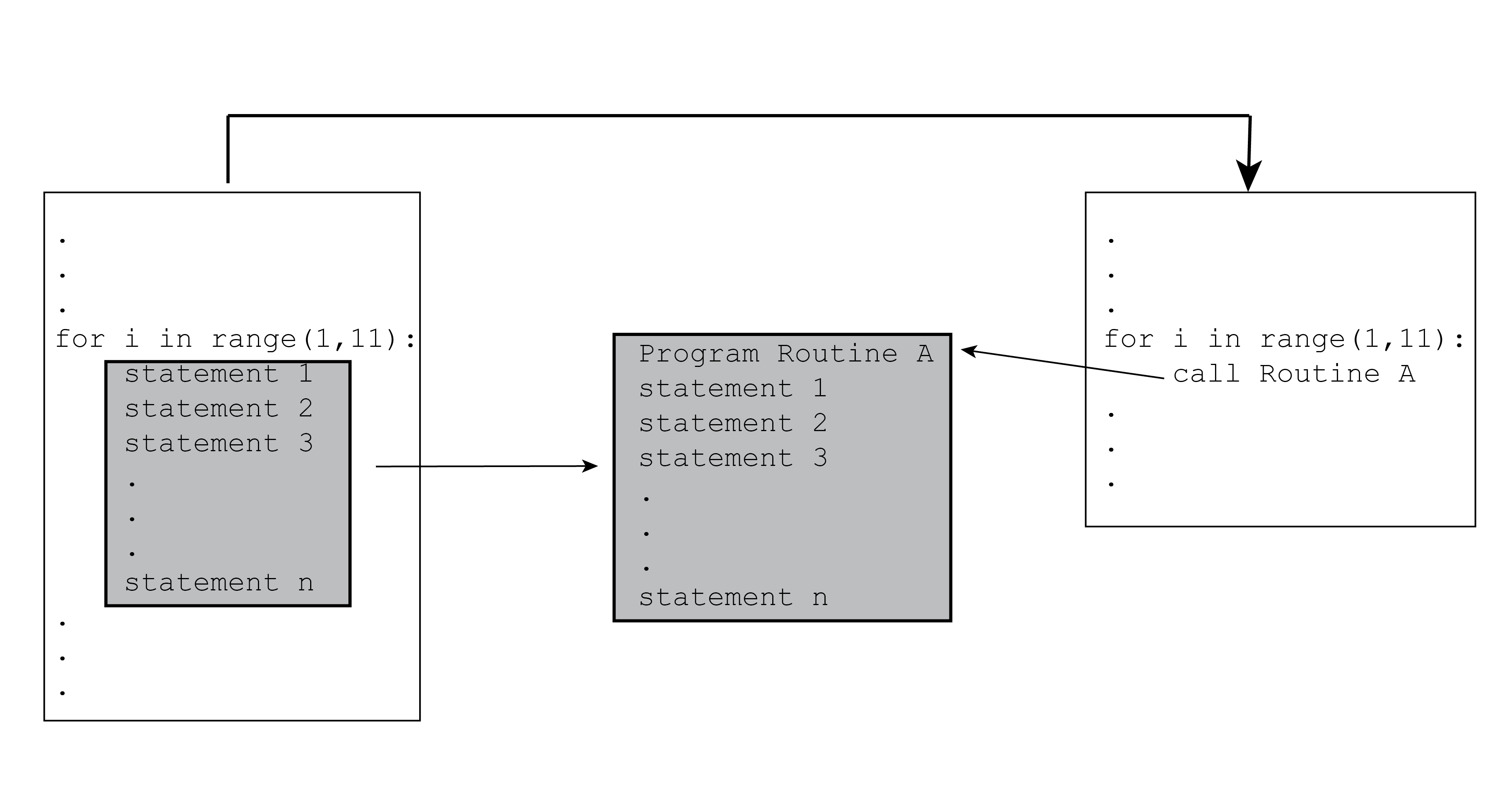
Python Functions as a Program Routine
The basic structure of a Python function definition is
def function_name(p1, p2, p3):
statement 1
statement 2
.
.
.The function definition begins with the header statement def, and the function name can be any legal Python variable name. The variable names in the parentheses are called parameters, which represent values that will be passed to the function when it is called. All statements inside the function definition comprise a suite (or block) of code and must all be indented by the same amount.
The parameter names, p1, p2, and p3, above are simply placeholders. They will be assigned actual values when the function is called from the main program. Consider the following example.
var1 = 10
var2 = 20
var3 = 30
function_name(var1, var2, var3)When the function is called, the parameters p1, p2, and p3 get replaced by the values in the variables var1, var2, and var3. Values that get passed to a function when it is called are arguments. The placeholder names appear in the function definition, and those placeholders get replaced by corresponding argument values when the function is called.
Python functions must be defined before they are called in a statement. Function definitions typically appear at the top of a program.
Value-returning Functions
In mathematics, the function notation, \(f\left(x\right)\) indicates a value that depends on the value of x for its definition. If you see \(f\left(x\right)\) in a mathematical statement, you can imagine it being replaced by the appropriate value. Similarly, value-returning functions get replaced by a value generated by the function in a statement containing the function. The returned value is indicated in the function definition through the use of the keyword return. The following code shows an example of a value-returning function.
def factorial(n):
f = 1
for i in range(1,n+1):
f = f*i
return f
# Main Program
print(factorial(4))The output of the print function is 24 in this example.
Non-value-returning Functions
As the name suggests, a non-value-returning function does not return a value when it is called in a statement; instead, it is called because of side effects that occur when the function is executed. For example, a non-value returning function might cause specific messages to be printed out. Figure 3 shows an example. Note that the function greeting(name) has no return statement, but it still has an effect.
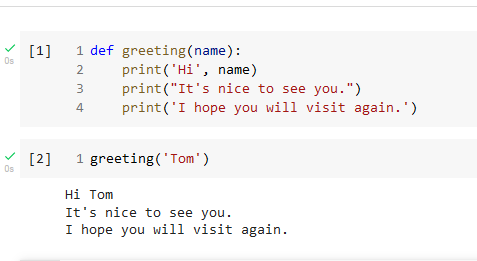
Strictly speaking, the non-value-returning function will return a value: None, but we will treat such functions as truly non-value-returning.
Function Parameters and Arguments
Parameter Passing
The variable names used in the parameter list of a function definition are placeholders. They get replaced by actual argument values when the function is called in a statement. Consider the following simple function.
def f(n1, n2):
t = 3.1415*(n1 + 2.0*n2)
return tThe main program contains the following statements
v1 = 3.0
v2 = 4.0
print(f(v1, v2))When the function f is called in the print statement, the parameters n1 and n2 in the function definition get replaced by the arguments v1 and v2. The call to f in the print statement results in the display of the number 34.56. The parameters are replaced by the arguments based on the order. If later in the main program, the following code is executed
print(f(v2,v1)the number 31.42 will be displayed.
Keyword Arguments
In the above example, values were assigned to function parameters using the position of the arguments in a function call. The technical term for such arguments is positional arguments. Values can also be assigned to parameters using parameter names. This approach is called keyword arguments. For the function \(f\) defined above, the following call to the function would result in 34.56 being displayed.
v1 = 3.0
v2 = 4.0
print(f(n2=v2, n1=v1))If you use both positional and keyword arguments to assign values to parameters in a function call, the positional arguments must all be assigned first.
Default Arguments
Default values can be assigned to a function parameter when the function is defined. The following code gives an example.
def f(n1=3, n2=4):
t = 3.1415*(n1 + 2.0*n2)
return t
print(f())The code will display 34.56 even though no arguments were provided to the function.
Variable Scope
The scope of a variable is the block of code in which the variable is defined, can be used, and can be modified. In a Python program that contains function definitions, variables can have either local or global scope. A local variable, or a variable with local scope, is defined and used within a function. A global variable, or a variable with global scope, is defined outside of a function. To explore the difference, consider the following short program.
def f1(n):
t1 = 2*n
t2 = t1 + 3
return t2
def f2(n):
t3 = 2*n + global_v
return t3
global_v = 5
print(f1(global_v))
print(f2(global_v))The first print statement displays the number 13, and the second print statement displays 15. Note that the variable global_v was not passed to function f2, but since it was defined outside of a function, it will have the value five everywhere in the program. global_v is a global variable or has global scope.
Now, after executing the above code, suppose we execute
print(t1)The result will be an execution error because the variable t1 was defined in function f1, not outside it, so it is available only within f1. t1 is a local variable or has local scope.
Computational Problem Solving: Temperature Conversion – Function Version
The problem described at the beginning of the chapter was to revise the temperature conversion program from Chapter 3 so that the following pieces were performed in functions rather than in the main program.
request a temperature to convert from the user
request the final temperature scale to be used
perform the actual temperature conversion calculation
Analysis
The critical analysis for this problem was performed in Chapter 3, where we collected all required conversion equations, Equations 3.1a-3.1f. We can use the test data in Table 3.5 to determine if our revised program is working correctly.
Design
We provide a revised pseudocode version of the temperature conversion program in Figure 4.
PROGRAM temperature_conversion
Print a program greeting
submitted_temperature, submitted_scale = request_temperature()
converted_scale = request_converted_scale(submitted_scale)
converted_temperature =
calculate_converted_temp(submitted_temperature,
submitted_scale, converted_scale)
Print out converted_temperature
ENDPROGRAMData structures used in the revised program are listed in Table 1.
| Data Structure | Type | Description |
|---|---|---|
| submitted_temperature | float variable | temperature submitted by the user |
| submitted_scale | string variable | scale for submitted_temperature |
| converted_temperature | float variable | the converted temperature |
| converted_scale | string variable | scale for converted_temperature |
The revised pseudocode for the program contains three functions. We must create pseudocode versions for each of those functions. These are contained in Figure 5, Figure 6, and Figure 7.
FUNCTION request_temperature
INPUT: None
submission_is_incorrect = True
scale_request = "'C' for Celsius, 'F' for Fahrenheit,
'K' for Kelvin "
WHILE submission_is_incorrect DO
Print request for temperature
Get temperature and convert to float (defines
submitted_temperature)
print request for scale
get scale (defines submitted_scale)
IF ((submitted_scale == 'C') and
(submitted_temperature >= -273.15))
submission_is_incorrect = False
ELSE IF ((submitted_scale == 'F') and
(submitted_temperature >= -459.67))
submission_is_incorrect = False
ELSE IF ((submitted_scale == 'K') and
(submitted_temperature >= 0)):
submission_is_incorrect = False
ELSE
print('Incorrect submitted temperature. Try again.')
ENDIF
ENDWHILE
OUTPUT submitted_temperature, submitted_scale
ENDFUNCTIONFUNCTION request_converted_scale
INPUT: submitted_scale
submission_is_incorrect = True
WHILE submission_is_incorrect DO
Print the request for the temperature scale
Get scale from user (defines converted_scale)
IF ((submitted_scale == 'C') and
(converted_scale == 'F' or converted_scale == 'K'))
submission_is_incorrect = False
ELIF ((submitted_scale == 'F') and
(converted_scale == 'C' or converted_scale == 'K'))
submission_is_incorrect = False
ELIF ((submitted_scale == 'K') and
(converted_scale == 'C' or converted_scale == 'F'))
submission_is_incorrect = False
ELSE
print('There is a problem with your submission.')
ENDIF
ENDWHILE
OUTPUT converted_scale
ENDFUNCTIONFUNCTION calculate_converted_temp
INPUT: submitted_temperature, submitted_scale, converted_scale
IF submitted_scale == 'C':
IF converted_scale == 'F'
# convert Celsius to Fahrenheit
converted_temperature = submitted_temperature*9.0/5.0 +
32.0
ELSE
# convert Celsius to Kelvin
converted_temperature = submitted_temperature + 273.15
ENDIF
ELIF submitted_scale == 'F':
IF converted_scale == 'C'
# convert Fahrenheit to Celsius
converted_temperature = (submitted_temperature –
32.0)*5./9.
ELSE
# convert Fahrenheit to Kelvin
converted_temperature = (submitted_temperature –
32.0)*5.0/9.0 + 273.15
ENDIF
ELSE
IF converted_scale == 'C'
# convert Kelvin to Celsius
converted_temperature = submitted_temperature - 273.15
ELSE
# convert Kelvin to Fahrenheit
converted_temperature = (submitted_temperature –
273.15)*9.0/5.0 + 32.0
ENDIF
ENDIF
OUTPUT converted_temperature
ENDFUNCTIONImplementation
The Python implementation of the three functions described above is straightforward and can be seen in Figure 8, Figure 9, and Figure 10. With those function definitions, the main program becomes short and very clear in its structure, as shown in Figure 11.
def request_temperature():
scale_request = "'C' for Celsius, 'F' for Fahrenheit, 'K' for Kelvin "
submission_is_incorrect = True
while submission_is_incorrect:
submitted_temperature = float(input('Submit a temperature'))
print('Specify the scale of your submitted temperature: ')
submitted_scale = input(scale_request)
if ((submitted_scale == 'C') and (submitted_temperature >= -273.15)):
submission_is_incorrect = False
elif ((submitted_scale == 'F') and (submitted_temperature >= -459.67)):
submission_is_incorrect = False
elif ((submitted_scale == 'K') and (submitted_temperature >= 0)):
submission_is_incorrect = False
else:
print('Incorrect submitted temperature. Try again.')
return submitted_temperature, submitted_scaledef request_scale(submitted_scale):
print('What scale should be used for the converted temperature?')
scale_request = "'C' for Celsius, 'F' for Fahrenheit, 'K' for Kelvin "
converted_scale = input(scale_request)
submission_is_incorrect = True
while submission_is_incorrect:
if ((submitted_scale == 'C') and
(converted_scale == 'F' or converted_scale == 'K')):
submission_is_incorrect = False
elif ((submitted_scale == 'F') and
(converted_scale == 'C' or converted_scale == 'K')):
submission_is_incorrect = False
elif ((submitted_scale == 'K') and
(converted_scale == 'C' or converted_scale == 'F')):
submission_is_incorrect = False
else:
print('There is a problem with your submission.')
converted_scale = input(scale_request)
return converted_scaledef calculate_converted_temp(submitted_temperature, submitted_scale,
converted_scale):
if submitted_scale == 'C':
if converted_scale == 'F':
# convert Celsius to Fahrenheit
converted_temperature = submitted_temperature*9.0/5.0 + 32.0
else:
# convert Celsius to Kelvin
converted_temperature = submitted_temperature + 273.15
elif submitted_scale == 'F':
if converted_scale == 'C':
# convert Fahrenheit to Celsius
converted_temperature = (submitted_temperature - 32.0)*5./9.
else:
# convert Fahrenheit to Kelvin
converted_temperature = (submitted_temperature - 32.0)*5.0/9.0 + 273.15
else:
if converted_scale == 'C':
# convert Kelvin to Celsius
converted_temperature = submitted_temperature - 273.15
else:
# convert Kelvin to Fahrenheit
converted_temperature = (submitted_temperature - 273.15)*9.0/5.0 + 32.0
return converted_temperature# Main Program
# Display program greeting
print('Welcome to the Temperature Scale Conversion Program!')
print('This program will request that the user submit a temperture.')
print('Next, it requests the converted scale.')
print('Finally, it prints out the converted temperature.')
submitted_temperature, submitted_scale = request_temperature()
converted_scale = request_scale(submitted_scale)
converted_temperature = calculate_converted_temp(submitted_temperature,
submitted_scale,
converted_scale)
# print out the result
s1 = format(submitted_temperature, '.2f')
s2 = format(converted_temperature, '.2f')
print(s1, submitted_scale, ' is ', s2, converted_scale)Testing
Test data listed in Table 5 from chapter 3 will be used to test the revised program. The complete code for the revised program is contained in the file Ch6TempConvProg.py. The test results for the program are listed in Table 2. The results provide evidence that the program works according to the requirements.
| Submitted Temperature | Converted Temperature | |||
|---|---|---|---|---|
| T | Scale | T | Scale | Program Output |
| -300 | C | Error | error detected | |
| -150 | C | -238 | F | -238 |
| -150 | C | 123.15 | K | 123.15 |
| 0 | C | 32 | F | 32 |
| 0 | C | 273.15 | K | 273.15 |
| -500 | F | Error | error detected | |
| -400 | F | -240 | C | -240 |
| -400 | F | 33.15 | K | 33.15 |
| 0 | F | -17.78 | C | -17.78 |
| 0 | F | 255.37 | K | 255.37 |
| -100 | K | Error | error detected | |
| 0 | K | -273.15 | C | -273.15 |
| 0 | K | -459.67 | F | -459.67 |
| 150 | K | -123.15 | C | -123.15 |
| 150 | K | -189.67 | F | -189.67 |
Exercises
1. T/F: A user-defined function can be called as many times as is necessary in a program.
2. When a function is defined, the variable names appearing in the parentheses are called _________.
3. When a function is called in the main part of a program, the values passed to it are called _______.
4. What kind of function must contain a return statement?
- any function
- value-returning function
- non-value-returning function
5. A non-value-returning function can perform useful work through ______________.
6. T/F: A value-returning function can only return one value at a time.
7. When a function call contains no keyword arguments, then the correspondence between arguments and function parameters is determined by the __________ of the arguments.
8. A program routine is
- the identifier in a function header
- a named group of instructions in a program
- a built-in function of a programming language
- the arguments passed from a function call
9. A formal parameter in a function is
- a placeholder name used in the function header, inside parentheses
- a value passed to the function in a function call
- the keyword def in a function definition
- a variable name that appears in the calling program for a function
10. Consider the following code
def a_function(p1, p2):
t = p1*p2
return t
# Main Program
num1 = 10.0
print(a_function(num1, 20.0)What is the scope of variable t in a_function?
Program Modification Problems
1. One of the main techniques used in developing a computational solution to a problem is abstraction. The primary technique for implementing abstraction in code is to define functions that solve a small part of the problem. Defining functions is especially useful when a certain process must be repeated many times across more than one program. The function definition can be reused in multiple programs.
This exercise will give you some practice in defining your own Python function.
You need to define a Python function that accepts an integer N as an argument and then adds all the integers from 1 to N and returns the value. The main program should ask the user for an integer, and then it should print out the result of the function. The code shown below is a starting point for your solution. Make sure to
Change the welcome message so that it is appropriate to the problem.
Define the function that calculates that does the calculation.
Prints out the user-defined integer and the sum with an appropriate message. This should be done in the Main Program.
"""
Program Name: Chapter 6 Prog Mod Prob 1
Author: C.D. Wentworth
version: 8.10.2022.1
Summary: This program will request that the user enter
a positive integer and prints it out.
"""
# Function definition
# Main Program
# Display program welcome
print('This program will request a number from the user.')
# Get an integer
user_number = int(input('Enter a positive integer: '))
while (user_number-int(user_number)) != 0 or (user_number <= 0):
user_number = int(input("Please enter a positive integer: "))
print('You entered N =', user_number)2. Modify the Chapter 6 Temperature Conversion Program discussed in the Computational Problem Solving: Temperature Conversion – Function Version section to include the Rankine scale in addition to Celsius, Fahrenheit, and Kelvin scales. Start with the code in the file
Ch6TempConversionProgram.py.
Program Development Problems
1. Write a program to produce a table of equivalent temperatures using the Kelvin, Celsius, Fahrenheit, and Rankine scales. Produce the columns in the order just described. Start with 0 [K] and go up to 375 [K] with a 5-degree increment. The numbers should be formatted to have two decimal places. Label each of the columns appropriately. The table should be written out to a tab-delimited text file.